Correspondingly, the density fluctuations follow the Gumbel distribution of extreme value statistics that is clearly distinguishable from a Gaussian distribution, which would arise in case of a homogeneous galaxy spatial configuration. A Gumbel distribution decays slower than a Gaussian, implying that large fluctuations are more probable than for a Gaussian process. There are thus important similarities between the galaxy distribution and critical systems of statistical physics, at least of scales smaller than 100 Mpc.
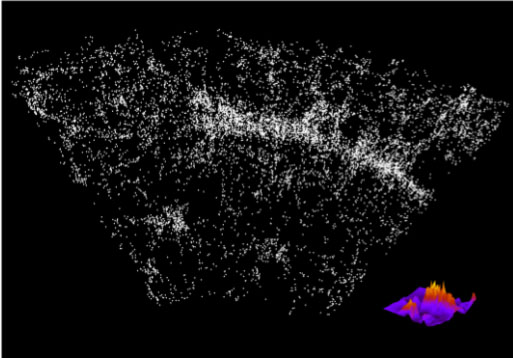
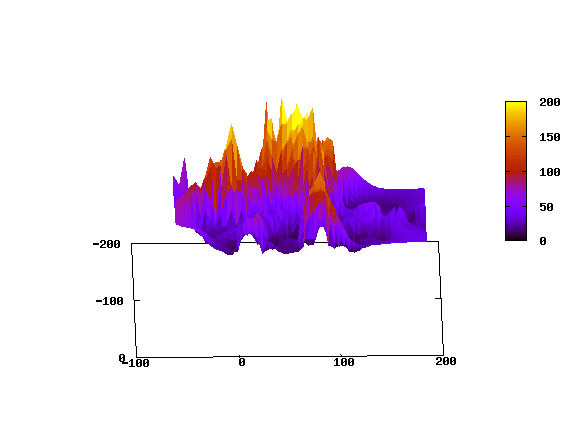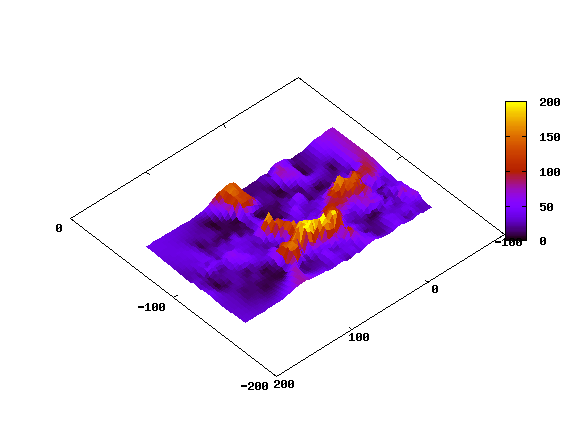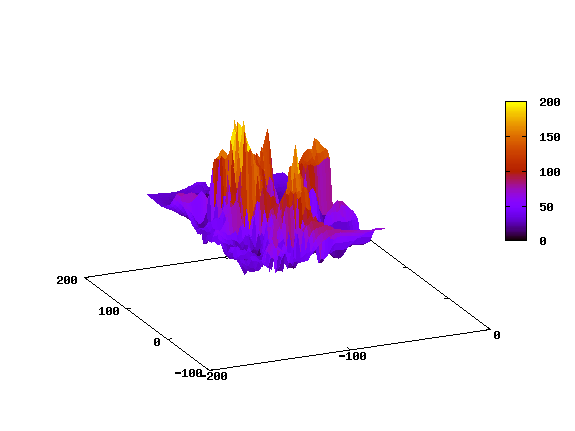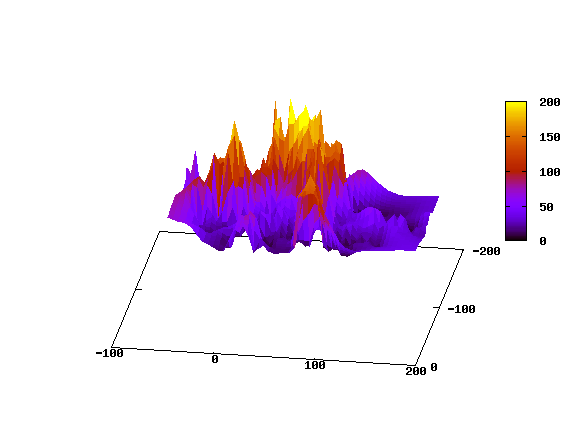
Below there is a reconstruction of the three dimensional fluctuation field in the SDSS survey. A larger scale structure, the Great Wall in this case, appears as a mountain chain, i.e a spatially extended structure.
Whether or not, on larger scales, correlations decay and the distribution crossovers to uniformity, is still matter of considerable debate. The principal questions concern indeed the nature of galaxy structures, the type of correlations and their spatial extension and the statistical properties of fluctuations distribution. The clarification of these points is crucial for the testing of cosmological models of structure formation. There is indeed a intense debate in the field stimulated by our results. For instance Steven Weinberg in his book “Cosmology” (2008) Oxford University, at pg.1 (first sentence) writes
The visible universe seems the same in all directions around us, at least if we look out to distances larger than about 300 million light years. (see K. K. S.Wu, O. Lahav, and M. J. Rees, Nature 397, 225 (January 21, 1999). For a contrary view, see P. H. Coleman, L. Pietronero, and R. H. Sanders, Astron. Astrophys. 200, L32 (1988): L. Pietronero, M. Montuori, and F. Sylos-Labini, in Critical Dialogues in Cosmology, (World Scientific, Singapore, 1997): 24; F. Sylos-Labini, F. Montuori, and L. Pietronero, Phys. Rep. 293, 61 (1998)).
The specific problem which initiated my research was the study of the clustering properties of galaxies as revealed by large redshift surveys, a context in which concepts of modern statistical physics (e.g. scale-invariance, fractality, etc.) found ready application. We have then considerably broadened the range of problems in cosmology which we have addressed, treating in particular more theoretical issues about the statistical properties of standard cosmological models and attempting to propose some theoretical models. What is common to all this research is that it is informed by a perspective and methodology which is that of statistical physics. Beyond my close collaborators in this activity (Luciano Pietronero, Michael Joyce, Andrea Gabrielli) I have collaborated with both well-known statistical physicists, as Phil Anderson (Princeton), Jean Pierre Eckmann (Geneva), and Joel Lebowitz (Rutgers) and cosmologists as Ruth Durrer (Geneva), Martin Lopez Correidoira (IAC Las Canarias), and Helene Di Nella-Courtois (Lyon). I can say that, beyond its specific scientific content, this activity has an underlying key-point: such interdisciplinary research is an exciting playground for statistical physics, and one which can bring new and useful insights into cosmology and astrophysics
Francesco sylos labini 