In astrophysics, to calculate the mass of a celestial body or a system of bodies, such as the Sun or our galaxy, there are essentially two methods: on one hand, one can measure the velocity that characterizes their motion, or on the other hand, one can measure the distortion of light they induce in distant sources, exploiting the gravitational lensing effect. In the first case, to find the mass from a velocity, it is necessary to make a key assumption: that the system is in a state of steady equilibrium.
Let’s consider the Solar System: the planets orbit around the Sun with velocities that decrease with distance. Assuming that the system has reached a sort of dynamic equilibrium, knowing the distance of a planet, denoted as R, from the Sun and its rotational velocity, denoted as v, we can calculate the mass of the Sun, denoted as M, using a formula that describes the equilibrium between the centrifugal force due to rotation and the centripetal force due ti gravity
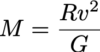
This same relation can be used to get the velocity if the mass and the distance are known .
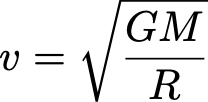
o calculate the mass of a celestial body or a system of bodies, such as the Sun or our galaxy, in astrophysics, there are essentially two methods. One way is to measure the velocity that characterizes their motion, and the other is to measure the distortion of light they induce in distant sources, using the gravitational lensing effect.
In the case of the Solar System, the planets orbit around the Sun with velocities that decrease with distance. Assuming that the system has reached a sort of dynamic equilibrium, knowing the distance of a planet (R) from the Sun and its rotational velocity (v), we can calculate the mass of the Sun (M) using a formula that describes the equilibrium.
The rotational velocity of the planets decreases with the inverse square root of the distance. This famous relationship was discovered by Kepler for the case of the Solar System, and the velocity that obeys this law is called Keplerian velocity.
A similar procedure is adopted to calculate the mass of our galaxy. The velocities and distances of stars or gas are measured in relation to their masses. If the mass of the galaxy were only the luminous mass, it would be expected that at sufficiently large distances from the center, the rotational velocity would follow the Keplerian law. However, it has been observed that for many galaxies, the velocity remains constant with distance, meaning that the rotation curve is flat. To explain this observation, a model was introduced, assuming that a significant portion of the mass, the majority of it, is dark matter. Dark matter does not emit electromagnetic radiation and cannot be directly observed. It is assumed to be distributed in a spherical halo around the center, so the mass is not concentrated in the center as in the case of the Solar System but is spread over a much larger volume. Assuming that the mass increases with radius and applying the formula mentioned above, it is found that the velocities remain constant.
In this way, it is found that dark matter, for a typical spiral galaxy like the Milky Way, must have a mass between ten and a hundred times greater than the visible mass. It is distributed in a spherical halo and does not rotate in a nearly flat disk like the luminous matter. For dynamic equilibrium to occur, dark matter must have an isotropic velocity distribution. This means that it moves randomly in all directions with an average velocity of zero but with a velocity dispersion that balances the gravitational force. To achieve this, dark matter must also have a crucial difference from luminous matter, it must not dissipate energy in the form of radiation when it heats up during gravitational compression. Many “exotic” particles have been hypothesized to fulfill this role, but despite significant experimental efforts, such as experiments in the Gran Sasso laboratory, no particle that can play this role has been observed yet.
By studying the rotation curves of our galaxy and distant galaxies, an interesting property has been noticed. While the radiation emitted by stars is highly concentrated in the central region, the emission of molecular hydrogen (HI), observable through the 21cm line, extends much farther. The distribution of HI can be observed using radio telescopes, and from this, the contribution of HI to the mass and hence to the rotation curve, the velocity as a function of distance if only molecular hydrogen were present, can be calculated. The interesting observation is that this rotation curve is very similar to the one observed when considering the total mass, not just the hydrogen mass, which represents a small fraction of the luminous mass due to stars (the latter can also be measured from the observation of infrared emission). In simple terms, it is observed that by multiplying the rotation curve obtained considering only HI by a factor of about 10 (but with significant variability from galaxy to galaxy), the total rotation curve is obtained. This fact suggests that molecular hydrogen is a “proxy” for the total mass distribution, beyond the luminous mass of stars. This means that where one atom of HI is observed, there should be ten more that do not emit the 21cm line. If this is the case, it could explain the rotation curve of all galaxies that are part of the best available sample for 21cm line observations, the THINGS sample.
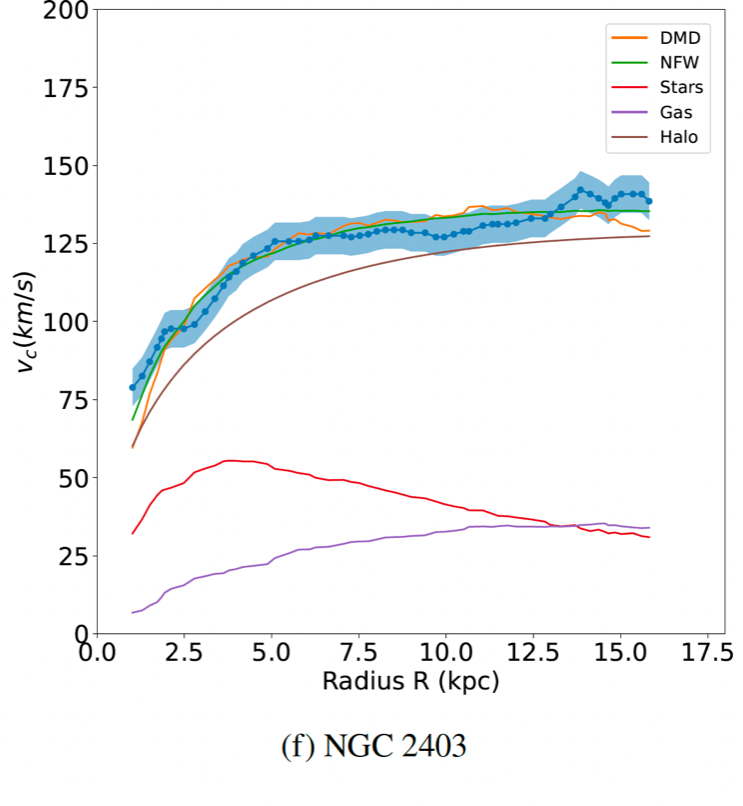
In the figure, the case of the galaxy NGC 2403 is illustrated: the red curve represents the rotation curve due to stars only, the purple curve represents the rotation curve due to molecular hydrogen, and the blue points are the observational data with error bars. By multiplying the purple curve by a factor of about ten, the orange curve is obtained, which explains the observational data well. The green curve represents the rotation curve obtained in the usual model where dark matter is distributed in a spherical halo.
If the matter were distributed like molecular hydrogen, it should be in the disk rather than in a spherical halo and should rotate like the luminous matter. Additionally, being confined to the disk and not dispersed in a spherical halo around it, it should contribute much less mass compared to the case of a spherical halo. For example, in our galaxy, there would be a need for about twice the luminous mass instead of eight times as in the case of a spherical halo. This dark matter, having properties similar to ordinary matter, could be composed of cold ordinary matter. It is known that cold hydrogen clouds (below 15 Kelvin) do not emit the 21cm line and thus would be electromagnetically invisible. This situation makes their direct observation impossible. However, it is in principle possible to distinguish whether a galaxy has a large mass in a spherical halo or a smaller mass contained in a disk through the effects of gravitational lensing. Our research group is moving in this direction: there are still no observations with the required precision, but the currently orbiting space telescopes will soon provide the necessary data to resolve the dilemma.
Some references
The Tully-Fisher relation and the Bosma effect, Monthly Notices of the Royal Astronomical Society, Volume 527, Issue 2, January 2024, Pages 2697–2717, https://doi.org/10.1093/mnras/stad3278, Francesco Sylos Labini, Giordano De Marzo, Matteo Straccamore, and Sébastien Comerón
